Un
modello previsionale quantitativo è semplicemente un processo di
calcolo che prevede l’inserimento di un insieme di dati di input
e che, sulla base di regole predefinite, restituisce in output delle previsioni.
In questo breve approfondimento costruiremo un semplice modello di previsione
del trend per il mercato azionario americano. Lo scopo è quello
di mostrare cosa sono, come funzionano, come si devono utilizzare e quale
tipo di insidie nascondono i modelli quantitativi.![]()
Costruiremo quello che tecnicamente si chiama “modello
di regressione polinomiale di grado 6”. A dispetto di
un nome che mette un po’ in soggezione, scopriremo che si tratta
di una metodologia piuttosto semplice da implementare. Ecco, in sintesi,
il percorso che seguiremo:![]()
1 –
predisposizione della serie storica dei prezzi di chiusura dell’indice
S&P 500
2 – costruzione del modello di previsione del trend
3 – applicazione del modello ai dati storici
4 – valutazione dei risultati ottenuti e dell’affidabilità
del modello![]()
1 - I dati di partenza![]()
Prima di tutto occorre reperire la serie storica dei prezzi dell’indice
su cui vogliamo lavorare; in questo caso l’S&P 500. Allo scopo
è possibile riferirsi a numerosi siti internet fra i quali, certamente,
Google Finance e Yahoo Finance. I dati utilizzati per questa esercitazione
possono essere scaricati direttamente dal seguente
link.
Si tratta di tutte le chiusure settimanali dell'indice della borsa americana
S&P500 tra il 4 gennaio 2002 ed il 30 luglio 2009.![]()
2 - Costruzione del modello![]()
Il modello che costruiremo in questa esercitazione è, come detto,
un polinomio di regressione di sesto grado. In sostanza si tratta di costruire
una funzione matematica capace di mettere in relazione lo scorrere del
tempo (nell'esempio parliamo di settimane) con l'evoluzione del prezzo
dell'indice.
Osservando la serie storica vediamo che al termine della prima settimana
(siamo al 4/1/02) l'indice vale 1173; la settimana successiva scende a
1146 per poi calare ulteriormente a 1128 alla terza settimana e così
via.
Possiamo allora riscrivere la tabella dei prezzi basandoci sul numero
di settimane invece che sulla data nel seguente modo:![]()

Il passo successivo
consiste nella ricerca di una funzione matematica che associ al numero
della settimana il corrispondente livello di prezzo.
Se torniamo con la mente ai tempi delle scuole superiori, probabilmente
riusciamo a ricordare il concetto di funzione matematica del tipo
![]() (che si legge "y uguale ad effe di x") e a quello che chiamavamo
piano cartesiano (i classici asse x ed asse y).
(che si legge "y uguale ad effe di x") e a quello che chiamavamo
piano cartesiano (i classici asse x ed asse y).
Molto frequente era il caso della funzione ![]() che
si rappresenta con una retta inclinata positivamente. La logica è
molto semplice, dato un certo valore della x (che nel nostro caso potrebbe
essere il numero della settimana), si ricava il corrispondente valore
della y (il prezzo dell’indice) applicando la formula
che
si rappresenta con una retta inclinata positivamente. La logica è
molto semplice, dato un certo valore della x (che nel nostro caso potrebbe
essere il numero della settimana), si ricava il corrispondente valore
della y (il prezzo dell’indice) applicando la formula ![]() .
.
Se la funzione ![]() fosse
il nostro modello di previsione, allora potremmo generare delle previsioni
partendo semplicemente dal numero della settimana nella quale ci troviamo.
Se siamo alla settimana n° 150 e vogliamo conoscere il prezzo dell’indice
alla prossima settimana (la 151esima) ci basterà applicare la formula
ossia prezzo = 2x150 = 300
fosse
il nostro modello di previsione, allora potremmo generare delle previsioni
partendo semplicemente dal numero della settimana nella quale ci troviamo.
Se siamo alla settimana n° 150 e vogliamo conoscere il prezzo dell’indice
alla prossima settimana (la 151esima) ci basterà applicare la formula
ossia prezzo = 2x150 = 300![]()
Immaginiamo di applicare la funzione ![]() ai
dati storici. Alla settimana 1 il prezzo dovrebbe essere pari a 2 mentre
il valore osservato è 1173. Alla settimana 3 il prezzo sarebbe
6 (3x2=6), ben lontano dal valore osservato pari a 1128.
ai
dati storici. Alla settimana 1 il prezzo dovrebbe essere pari a 2 mentre
il valore osservato è 1173. Alla settimana 3 il prezzo sarebbe
6 (3x2=6), ben lontano dal valore osservato pari a 1128.
Evidentemente la funzione è inadeguata allo scopo. Ciò che
dovremo cercare è un qualcosa di più complesso che possa
davvero generare numeri realistici. A questo scopo la matematica ci viene
in aiuto con uno strumento noto come regressione polinomiale. Si tratta
di una metodologia che permette di modificare una funzione in modo tale
che sia il più possibile fedele ai dati osservati. Nel nostro caso
si tratta di fare in modo che la curva della funzione passi il più
possibile vicino ai punti sul grafico che rappresentano le osservazioni
del prezzo in ciascuna settimana.![]()
Vediamo un esempio concreto con i primi 20 dati della nostra serie
storica:![]()
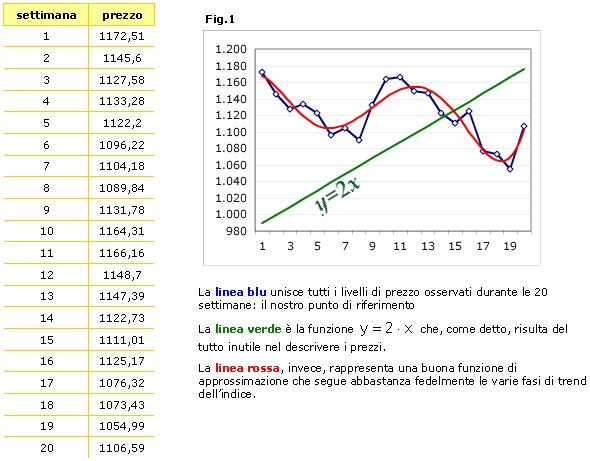
Polinomio di regressione![]()
La linea rossa sopra rappresentata è, per l’appunto, un polinomio
di regressione di grado 6 calcolato con il metodo dei minimi quadrati.
Tradotto in parole povere, si tratta di una funzione matematica (non molto
diversa dalla ![]() )
opportunamente manipolata in modo da farla passare il più possibile
vicino ai livelli di prezzo effettivamente osservati. Un polinomio di
grado 6 è ciò che alle scuole superiori chiamavamo equazione
di sesto grado ed assume la seguente forma:
)
opportunamente manipolata in modo da farla passare il più possibile
vicino ai livelli di prezzo effettivamente osservati. Un polinomio di
grado 6 è ciò che alle scuole superiori chiamavamo equazione
di sesto grado ed assume la seguente forma:
![]()
![]() La
logica è sempre la stessa: per ogni numero di settimana (x)
è possibile calcolare il corrispondente livello di prezzo (y)
utilizzando la relazione sopra descritta.
La
logica è sempre la stessa: per ogni numero di settimana (x)
è possibile calcolare il corrispondente livello di prezzo (y)
utilizzando la relazione sopra descritta.
Le lettere a,b,c,d,e,f,g sono dei numeri fissi (che prendono il nome di
“termini noti”) che dovranno essere
opportunamente scelti in modo da modellare la curva intorno al grafico
della serie storica da analizzare.
Il metodo dei minimi quadrati è, per l’appunto, quella tecnica
che consente di individuare il valore da attribuire ai termini noti per
essere certi di minimizzare le differenze tra i valori osservati e quelli
stimati dal polinomio.![]()
Nell’esempio precedente sono stati calcolati i termini noti ottimali
per far passare il polinomio generico di cui alla 1.1
il più possibile vicino ai 20 valori di prezzo osservati. Il risultato
è la linea rossa rappresentata in Fig.1 ed assume
la seguente formula:
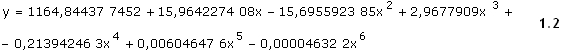
![]() Sostituendo
in questa formula alla x i numeri che vanno da 1 a 20 (le venti settimane)
è possibile calcolare il prezzo teorico previsto dal modello per
l’indice S&P500:
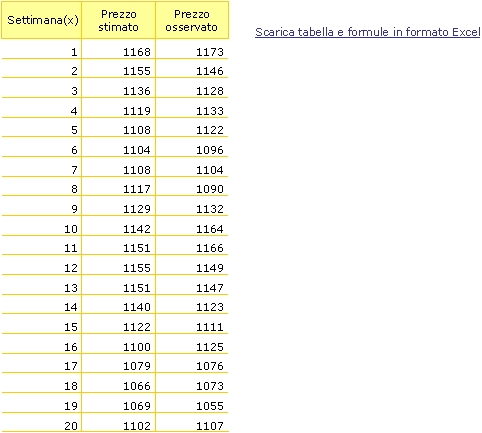
Sostituendo
in questa formula alla x i numeri che vanno da 1 a 20 (le venti settimane)
è possibile calcolare il prezzo teorico previsto dal modello per
l’indice S&P500:![]()
3 - Applicazione ai dati storici![]()
Il modello
di regressione polinomiale, per quanto teoricamente complesso da implementare,
risulta di facile utilizzo in quanto pienamente supportato da Excel. Nel
foglio di calcolo prelevabile da questo
link, viene fatto uso dello strumento “trendline” di Excel
per calcolare i parametri di un polinomio di regressione di grado 6 sull’intera
serie storica dell’indice S&P500.![]()
Il procedimento, peraltro piuttosto semplice, può essere osservato
in questa video
guida dedicata![]()
I parametri
ottenuti vengono poi utilizzati per ricostruire interamente la serie di
prezzi così come mostrato nell’esempio sulle prime venti
settimane. Dal momento che il meccanismo di costruzione del polinomio
è incentrato sulla minimizzazione degli errori nella replica dei
dati storici, è normale che la distanza fra ogni singolo prezzo
osservato e la corrispondente previsione non sia mai enorme.![]()
Ora che disponiamo di una funzione che associa al numero della settimana
il prezzo dell’indice possiamo ricavare ciò che ci eravamo
prefissati all’inizio: un modello di previsione del trend.
Supponiamo di trovarci alla settimana numero 1: il prezzo osservato è
1173, mentre il prezzo previsto per la settimana successiva (la numero
2) può essere ricavato utilizzando la funzione appena descritta:
prezzo atteso = 1359,65200235554 - 30,9537805188738x2 - 0,0062706566044x2^2
+ 0,00002842613920x2^3 - 0,00002842613920x2^4 -0,00000006157240x2^5+ 0,00000000005060x2^6
= 1300
La stima relativa alla seconda settimana formulata la settimana precedente
è pari a 1300 che, rispetto al 1173 di partenza evidenzia un’attesa
di trend rialzista. Il dato effettivamente osservato alla settimana 2,
tuttavia, è 1146 che, essendo inferiore al 1173 di partenza, smentisce
il modello configurando un trend decrescente dei prezzi osservati sul
mercato.
E’ possibile ripercorrere tutta la serie storica verificando, settimana
dopo settimana, se le previsioni di trend ottenute tramite l’applicazione
di questo modello, sarebbero state corrette oppure no. Scopriremo che,
con questo modello, avremmo indovinato il 56% dei trend settimanali dell’indice
S&P500.![]()
Per capire meglio quanto detto è possibile scaricare un apposito
foglio excel.



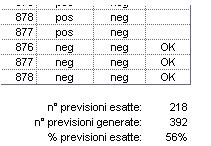 Infine
verifichiamo, per ciascuna settimana, se il trend previsto coincide con
quello osservato. Contando il numero di trend previsti correttamene (contrassegnati
da un “OK”) e rapportandolo alla totalità delle previsioni
formulate, otteniamo il tasso di successo del modello. In questo caso
56%
Infine
verifichiamo, per ciascuna settimana, se il trend previsto coincide con
quello osservato. Contando il numero di trend previsti correttamene (contrassegnati
da un “OK”) e rapportandolo alla totalità delle previsioni
formulate, otteniamo il tasso di successo del modello. In questo caso
56%
4 – Valutazione dei risultati ottenuti
e dell’affidabilità del modello – un’insidia
nascosta![]()
Per valutare correttamente i risultati ottenuti da un modello previsionale
è sempre importante definire con chiarezza le proprie aspettative.
In questo caso abbiamo sviluppato un modello di previsione del trend su
base settimanale. Il compito del nostro modello è quello di informarci,
al termine di una settimana di borsa, se, nel corso della settimana successiva,
il trend sarà positivo o negativo. Dal momento che le probabilità
di indovinare il trend lanciando semplicemente una moneta sono pari al
50% potremo essere soddisfatti del nostro modello solo se capace di fornire
indicazioni corrette in oltre la metà dei casi. Diversamente avremo
lavorato per niente e non disporremo di un modello migliore del lancio
della moneta.
In questo caso, una percentuale di successo del 56% ci offre qualcosa
in più del lancio di una monetina ma, naturalmente, non ci lascia
particolarmente soddisfatti.
Il modello implementato in questa esercitazione, infatti, è molto
semplice e ben lungi dall’essere un caso reale di modello previsionale
(i modelli sviluppati da nonsolofondi arrivano spesso a prevedere correttamente
oltre il 95% dei trend - ecco
alcuni esempi di successo).![]()
Ma vediamo qual è la preannunciata
insidia nascosta. Immaginiamo che il modello qui sviluppato
fosse stato capace di prevedere correttamente il 90% dei trend (e non
il 56% come invece abbiamo osservato).![]()
In questo caso sarebbe stato corretto affermare che le previsioni
di trend generate dal modello presentano un'affidabilità del 90%?
La risposta è ASSOLUTAMENTE NO!![]()
Non possiamo affermare ciò in quanto la precisione del modello
sarebbe soltanto il risultato del processo di ottimizzazione dei parametri
volto proprio a minimizzare i residui (ossia gli scostamente fra i valori
interpolati e quelli osservati sul mercato). Il 90% di precisione non
è, quindi, il risultato di un back test. Esso deriva dal fatto
che abbiamo utilizzato i dati storici disponibili per individuare il valore
ottimale per i paramentri del polinomio. E' naturale che, andando ad applicare
il polinomio sui medesimi dati storici, i risultati siano positivi.
Alla luce di quanto detto pare strano di aver ottenuto un tasso di successo
pari solo al 56%! In effetti la bassa qualità del modello dipende
unicamente dalla scelta del polinomio di grado 6 fatta a monte. Molto
probabilmente si sarebbero potuti ottenere risultati migliori con un polinomio
di grado maggiore o con una funzione esponenziale o altro ancora.![]()
Per questa ragione i risultati ottenuti dai nostri backtest sono davvero rappresentativi dell'affidabilità delle nostre previsioni.